


La vita di Pitagora
Nella scuola pitagorica scienza e filosofia , musica e religione si fondono inscindibilmente in una mistica contemplazione dell ‘ universo . Secondo Proclo Pitagora trasformò lo studio della matematica in una vera scienza , considerando le fondamenta di essa da un punto di vista più elevato ed indagandone i teoremi sotto un aspetto astratto ed intellettuale . Matematico e filosofo greco nato a Samo verso il 575 A.C. . A quarant’anni si stabilì a Crotone dove fondò una propria comunità di carattere religioso che prese il nome di Scuola Italica . Verso il 500 , una sommossa provocata dal partito democratico cacciò i pitagorici da Crotone . Pare che Pitagora sia riuscito a fuggire a Metaponto , ove morì qualche anno dopo . E’ difficile stabilire quali risultati siano dovuti a Pitagora personalmente e quali ai suoi discepoli ; il merito principale della scuola pitagorica è la fondazione della scienza dei numeri portata oltre le regole pratiche del calcolo . Pitagora è il celebre creatore di un sistema filosofico nel quale l’elemento primordiale non è di natura tangibile , ma un essere di ragione , cioè il numero , considerato come l ‘ essenza stessa delle cose.
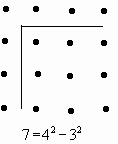
Le leggi della formazione della realtà sono , per i Pitagorici , quelle stesse della formazione dei numeri . I numeri sono rappresentati come collezioni di punti separati da spazio vuoto e distribuiti in ordine particolare a seconda dei casi . I numeri dispari , per esempio , sono rappresentati come punti disposti in modo da formare la figura della squadra del falegname ( lo gnomone ) . Nasce così l aritmetica figurata Essa indaga sui numeri tenendo presenti le figure geometriche che li rappresentano .
E’ facile dimostrare per questa via che ogni numero dispari è uguale alla differenza di due quadrati . Precisamente dei quadrati dei due numeri consecutivi di cui il numero dato è uguale alla somma .




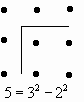

Pitagora e la religione
L’adesione di una scuola filosofica , come la pitagorica , a tali forme propriamente magiche , può suscitare meraviglia in chi sia stato partecipe del senso di elevato razionalismo che pervade la scuola ionica . Il cammino della vita è la filosofia , cioè lo sforzo verso la saggezza inteso come fattore di elevazione morale . Ed è caratteristico del genio greco che l’attività artistica e scientifica verso il bello ed il vero assumano qui un significato religioso . Oggi essi appaiono come sogni di menti ammalate ; ma , coprendo con la bandiera della << geometria mistica >> i frutti della pura ricerca scientifica , i Pitagorici ne facilitarono la diffusione anche fra coloro che non sarebbero stati in grado di apprezzare il valore di una scienza allora in fasce .
I numeri erano concepiti come punti , ossia come masse , ed erano di conseguenza concepiti come solidi e quindi il passaggio dal numero alle cose fisiche era ovvio .
L illimitato è il vuoto circondante il tutto ed il mondo nasce mediante una sorta di << inspirazione >> di questo vuoto da parte di un UNO ( la cui genesi non viene ben specificata ) . Il vuoto che entra con la inspirazione e la determinazione che l ‘ UNO produce inspirandolo dà origine alle varie cose ed ai vari numeri .
Il Divino e l’anima
I Pitagorici collegarono il Divino col numero . Non con il numero 1 ma con il numero 7 , il quale è reggitore e signore di tutte le cose , dio , unico , eterno , solido , immobile , uguale a se stesso , diverso da tutti gli altri numeri . Il 7 , all’interno della sacra decade , non è generato ( non è il prodotto di due fattori ) , è un numero primo , né genera altri numeri , e ciò che non è generato e che non genera è immobile .
I numeri principio della realtà
Per Pitagora i numeri sono il principio di tutte le cose . Per i pitagorici il problema essenziale era quello di cogliere il modo con cui dalla collezione di più unità si generano tutti gli esseri . Le leggi della formazione dei numeri venivano considerate come leggi della formazione delle cose , e si riteneva di potere trovare in esse la vera ragione esplicativa del mondo fisico e morale .
Questa presenza di significati multipli finiva con l’infondere ai numeri , ed a certuni di essi in particolare , un vero e proprio valore
magico-simbolico .Il numero
1 se ne stava per conto proprio come sorgente di tutti i numeri e rappresentava la ragione ( il numero 1 veniva considerato come parimpari servendo a generare sia i numeri pari che i numeri dispari ) .Il numero 2 rappresentava la donna , il numero 3 rappresentava l’uomo , il numero 4 rappresentava la giustizia perché è il prodotto di due numeri uguali .
Il numero 5 rappresentava il matrimonio essendo la somma del primo numero dispari il 3 ( che rappresentava l’uomo ) col primo numero pari il 2 ( che rappresentava la donna ) .
La contemplazione dei numeri veniva a possedere un doppio aspetto :
scientifico e mistico .Ciascun numero possedeva a sua volta attributi suoi particolari . Il più sacro di tutti era il numero dieci o tetractys , poiché esso rappresentava il numero dell’universo . Infatti conteneva la somma di tutte le dimensioni geometriche possibili . Un punto è il generatore delle dimensioni , due punti determinano una linea ad una dimensione ( retta ) tre punti ( non allineati ) determinano un triangolo con un’area a due dimensioni ,e quattro punti ( non giacenti su uno stesso piano ) determinano un tetraedro con un volume a tre dimensioni .
La somma dei numeri ( 1+2+3+4=10 ) rappresentanti tutte le dimensioni è il venerato numero dieci .
|
Il numero perfetto fu identificato con il |
|
La raffigurazione mostra che il numero ![]() è uguale a
è uguale a ![]() . Ma c’è di più
. Nella decade sono contenuti ugualmente il pari ( quattro numeri
pari : 2,4,6,8 ) ed il dispari ( quattro numeri dispari : 3,5,7,9 ) . La
decade contiene 4 numeri primi ( 2,3,5,7 ) e 4 numeri composti ( 4
, 6 , 8 , 9 ) .
. Ma c’è di più
. Nella decade sono contenuti ugualmente il pari ( quattro numeri
pari : 2,4,6,8 ) ed il dispari ( quattro numeri dispari : 3,5,7,9 ) . La
decade contiene 4 numeri primi ( 2,3,5,7 ) e 4 numeri composti ( 4
, 6 , 8 , 9 ) .
L ‘ uno equivale al punto , il 2 alla linea , il 3 al triangolo ( e quindi alla superficie ) , il 4 alla piramide ( e quindi ad un generico solido ) : i punti , le linee , le superfici , i solido sono in grado di generare tutte le cose che esistono in natura .
Seconde le vedute di Pitagora i 4 numeri della sacra tetracktys sono in grado di generare tutta la realtà che ci circonda .
La teoria delle monadi : aritmetica e mistica dei numeri
In quale modo il numero può essere considerato come una specie di materia , al pari dell’acqua o dell’aria o del fuoco
? La formula paradossale << le cose sono numeri >> viene a significare che ogni porzione di materia è composta di elementi o punti materiali , di piccola ma non nulla grandezza ; e che dalla configurazione ( numero ed ordine ) di codesti punti , fra loro identici e qualitativamente indifferenti , dipendono tutte le proprietà e differenze apparenti dei corpi .Per i pitagorici la sostanza primitiva infinita dà origine alla materia propriamente detta per condensazione attorno ad un gruppo di punti o centri monadici . Intorno ad ogni centro monadico si forma un piccolo nucleo compatto , la monade , che rimane circondata e separata dalle altre monadi da qualcosa di rarefatto come l’etere .
Ogni numero si identificava con qualche attributo umano . Il numero uno rappresentava la ragione perché è immutabile ; il numero due l’opinione ; il numero quattro la giustizia perché è il primo quadrato perfetto , prodotto di due numeri uguali ; il numero cinque il matrimonio perché è l’unione del primo numero maschile e del primo numero femminile Qualcosa di analogo si trova , ed è molto strano , nella mitologia cinese , nella quale i numeri dispari erano i simboli di bianco , giorno , calore , sole , fuoco mentre i numeri pari rappresentavano il nero, la notte ,il freddo , la materia , l’acqua , la terra . I numeri erano disposti su una sacra tavoletta , chiamata LO-Chou , che , opportunamente usata , aveva proprietà magiche .
· Se partiamo da 1
la somma di un numero qualsiasi di numeri interi consecutivi è un numero
triangolare come indica la seguente figura : 
· La somma di una
successione di numeri dispari consecutivi dà sempre un numero quadrato come
indica la seguente figura  . Se
sommo n numeri dispari consecutivi trovo sempre il numero
. Se
sommo n numeri dispari consecutivi trovo sempre il numero ![]() :
: ![]()
· La somma di una
successione di numeri pari consecutivi dà sempre un numero rettangolare come
indica la seguente figura 
![]() Il numero
Il numero ![]() è il numero
rettangolare che si ottiene sommando i primi 3 numeri pari .. Se sommo n
numeri pari consecutivi trovo sempre il numero rettangolare
è il numero
rettangolare che si ottiene sommando i primi 3 numeri pari .. Se sommo n
numeri pari consecutivi trovo sempre il numero rettangolare ![]() :
:
|
Le linee diagonali della figura di un qualsiasi numero rettangolare ci dicono che qualsiasi numero rettangolare è uguale alla somma |
|
di due numeri triangolari uguali
.
|
Numeri naturali |
|
somma triangolare ; numeri triangolari |
|
Numeri dispari |
|
somma quadrata ; numeri quadrati |
|
Numeri pari |
|
somma rettangolare ; numeri rettangolari |
|
Contando per 3 |
|
somma pentagonale ; numeri pentagonali |
|
Contando per 4 |
|
somma esagonale ; numeri esagonali |
numeri pentagonali : ![]() numeri
esagonali :
numeri
esagonali : ![]()
|
|
Numeri pentagonali Per Per |
|
|
Numeri esagonali per per
|
Liberata del suo misticismo , la filosofia pitagorica conteneva l’idea fondamentale che soltanto attraverso il numero e la forma l’uomo possa afferrare la natura dell’universo . Questo concetto troviamo espresso nel pensiero scientifico di Filolao il migliore discepolo di Pitagora .
La discontinuità
Si dice che la scienza di Pitagora è una matematica del discontinuo , perché essa si fonda esclusivamente sui numeri interi e su ciò che può essere espresso con i numeri interi ( per esempio sulle frazioni ordinarie e non , invece , sui numeri irrazionali ) . Secondo essa , l’accrescimento di una grandezza procede per << salti discontinui >> essendo impensabile aggiungere qualcosa che sia minore dell’unità . Taluno giunge a riconoscere nelle teorie quantistiche moderne una sopravvivenza dell’antica eredità pitagorica sotto forma di concezione discontinua dell’energia .
Il secondo notevole contributo di Pitagora alla matematica ci
mette di fronte a dei problemi vitali nel mondo della matematica . Si tratta
della sua scoperta da cui fu umiliato e sconvolto , che i numeri naturali ![]() sono
insufficienti a costruire la matematica , anche nella forma rudimentale da lui
conosciuta . Prima di questa scoperta capitale egli aveva predicato , come un
profeta ispirato , che tutta la natura , l’universo intero, ogni cosa
matematica , fisica , metafisica , morale riposa sul modulo discreto dei
numeri naturali
sono
insufficienti a costruire la matematica , anche nella forma rudimentale da lui
conosciuta . Prima di questa scoperta capitale egli aveva predicato , come un
profeta ispirato , che tutta la natura , l’universo intero, ogni cosa
matematica , fisica , metafisica , morale riposa sul modulo discreto dei
numeri naturali ![]() e può essere
interpretato per mezzo di questi elementi datici da Dio. Dio , dichiarava
Pitagora , è numero , anzi meglio è << numero intero >>
.Una dura contraddizione distrugge le teorie matematiche , metafisiche e
filosofiche di Pitagora ma , contrariamente a certi suoi successori , egli
accetta infine la sua disfatta , dopo essersi sforzato , senza successo , di
sopprimere la scoperta che aveva distrutto la sua fede .
e può essere
interpretato per mezzo di questi elementi datici da Dio. Dio , dichiarava
Pitagora , è numero , anzi meglio è << numero intero >>
.Una dura contraddizione distrugge le teorie matematiche , metafisiche e
filosofiche di Pitagora ma , contrariamente a certi suoi successori , egli
accetta infine la sua disfatta , dopo essersi sforzato , senza successo , di
sopprimere la scoperta che aveva distrutto la sua fede .
Ciò che aveva fatto fallire la sua teoria è l’impossibilità di trovare due numeri interi tali che il quadrato dell’uno sia uguale al doppio del quadrato dell’altro . In termini geometrici possiamo dire che il rapporto tra il lato e la diagonale di un qualsiasi quadrato non può essere espresso dal rapporto di due numeri interi .
Con questa scoperta Pitagora fondò l’analisi matematica moderna .
Questo semplice problema ha dato origine a problemi concernenti i concetti matematici dell’infinito , dei limiti , della continuità , concetti che si trovano all’origine dell’analisi moderna .
I numeri amici o numeri amicabili
Due numeri interi a e b sono detti numeri
amicabili o numeri amici se a è la somma dei divisori di b
escluso b e b è la somma dei divisori di a escluso a . I più piccoli
numeri che formino una coppia del genere sono ![]() e
e ![]() .
.
I numeri perfetti
Un numero si dice perfetto se è uguale alla somma dei suoi divisori , escluso il numero stesso .
Sono numeri perfetti : ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
I numeri collega
Si chiamano numeri collega di classe n due numeri tali che ognuno di essi sia uguale alla somma delle cifre dell’altro elevata alla potenza n .
I numeri ![]() e
e ![]() sono numeri collega di secondo grado in quanto risulta :
sono numeri collega di secondo grado in quanto risulta :
![]()
![]()
I numeri ![]() e
e ![]() sono numeri collega di terzo grado in quanto risulta :
sono numeri collega di terzo grado in quanto risulta :
![]()
![]()
I numeri pitagorici
Si ricercano quelle terne di numeri interi ( naturali
) tali che il quadrato di uno di essi sia uguale alla somma dei quadrati degli
altri due . Con linguaggio moderno diremmo che si ricercano le soluzioni intere
dell’equazione a tre incognite ![]() .
.
Pitagora riesce a dare la formula per x dispari . In questo
caso si ottiene una terna pitagorica ponendo : ![]() ,
, ![]() ,
, ![]()
La formula per x pari è stata data da Platone .
Se x è pari abbiamo : ![]() ,
, ![]() ,
, ![]()
Terne pitagoriche e triangoli aritmetici
![]() [A]
è detta equazione pitagorica in quanto esprime la nota relazione fra i
lati di un triangolo rettangolo . Se x , y , z sono numeri interi
positivi che verificano la [A] , si dice che costituiscono una terna di
numeri pitagorici ed il corrispondente triangolo rettangolo è detto triangolo
aritmetico . Per risolvere l’equazione [A] per numeri interi ,
basterà trovare tutte le sue soluzioni intere positivi o meglio basterà
determinare le sue soluzioni primitive , cioè le soluzioni costituite da
numeri interi primi fra loro .
[A]
è detta equazione pitagorica in quanto esprime la nota relazione fra i
lati di un triangolo rettangolo . Se x , y , z sono numeri interi
positivi che verificano la [A] , si dice che costituiscono una terna di
numeri pitagorici ed il corrispondente triangolo rettangolo è detto triangolo
aritmetico . Per risolvere l’equazione [A] per numeri interi ,
basterà trovare tutte le sue soluzioni intere positivi o meglio basterà
determinare le sue soluzioni primitive , cioè le soluzioni costituite da
numeri interi primi fra loro .
Ogni terna pitagorica primitiva genera infinite terne pitagoriche .
Ricerca di tutte le terne pitagoriche
Se indichiamo con ![]() una costante di proporzionalità le precedenti formule possono essere scritte
nella seguente maniera :
una costante di proporzionalità le precedenti formule possono essere scritte
nella seguente maniera : 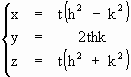 [B]
[B]
Abbiamo così trovato tutte le terne pitagoriche , cioè tutte le possibili soluzioni intere dell’equazione pitagorica [A] .
Proprietà delle terne pitagoriche
La somma delle terne che costituiscono una terna pitagorica è un numero pari . Infatti risulta :
![]()
Il prodotto delle misure dei tre lati di un triangolo
pitagorico è multiplo di ![]() .
Esempio
.
Esempio ![]()
![]()
Storia e leggenda del teorema di Pitagora
Come sappiamo il teorema di Pitagora recita . << in
ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente
alla somma dei quadrati costruiti sui due cateti >> . Il teorema di
Pitagora può essere esposto anche nella seguente forma . << in ogni
triangolo rettangolo l’area della superficie del quadrato che ha per lato l’ipotenusa
è uguale alla somma delle aree delle superfici dei quadrati che hanno come lato
i loro cateti >> . Avendo indicato con a e b le
lunghezze dei cateti di un triangolo rettangolo e con c quella dell’ipotenusa
, quanto ora affermato si traduce nella relazione : ![]() [1]
[1]
ossia si può scrivere una relazione tra numeri , collegata
alla figura costituita da un triangolo rettangolo . Secondo alcuni storici
antichi ( Plutarco , Diogene Laerzio ) fu Pitagora stesso ad enunciare il
famoso teorema che porta il suo nome . La leggenda dice che Pitagora comprese
tanto bene l’importanza della sua dimostrazione da ordinare una ecatombe ,
cioè il sacrificio di ![]() buoi , in
segno di ringraziamento e di gioia per avergli permesso una simile scoperta .
buoi , in
segno di ringraziamento e di gioia per avergli permesso una simile scoperta .
Convinti che Pitagora abbia dimostrato il teorema che porta il suo nome ci chiediamo : << come l’avrà dimostrato ? >> La dimostrazione del teorema di Pitagora , che di solito si studia a scuola non è di Pitagora , ma di Euclide come sappiamo da un certo Proclo << commentatore >> degli Elementi di Euclide .
Noi riteniamo che la dimostrazione originale di Pitagora sia
quella che ora esponiamo con l’aiuto di due figure . Nella prima figura è
disegnato un quadrato ![]() di lato
di lato ![]() , scomposto in un quadrato di lato a , un quadrato di lato b e 4 triangoli
rettangoli di lati a , b , c .
, scomposto in un quadrato di lato a , un quadrato di lato b e 4 triangoli
rettangoli di lati a , b , c .
Nella seconda figura consideriamo lo stesso quadrato ![]() che , questa volta , decomponiamo in modo diverso , precisamente lo decomponiamo
in 4 triangoli rettangoli di lati a , b , c ed in un quadrato di lato c .
Abbiamo due quadrati ( quelli grandi di lato
che , questa volta , decomponiamo in modo diverso , precisamente lo decomponiamo
in 4 triangoli rettangoli di lati a , b , c ed in un quadrato di lato c .
Abbiamo due quadrati ( quelli grandi di lato ![]() , uguali . Se da essi , tanto dall’uno quanto dall’altro , togliamo una
stessa area ( quella dei 4 triangoli rettangoli con cateti a , b ) , le parti
che restano avranno ancora area uguale . Ma le parti che restano sono , nella
prima figura , la somma dei quadrati dei cateti a e b , nella seconda il
quadrato dell'ipotenusa c . Il teorema di Pitagora è così dimostrato, con
tutta probabilità al modo di Pitagora .
, uguali . Se da essi , tanto dall’uno quanto dall’altro , togliamo una
stessa area ( quella dei 4 triangoli rettangoli con cateti a , b ) , le parti
che restano avranno ancora area uguale . Ma le parti che restano sono , nella
prima figura , la somma dei quadrati dei cateti a e b , nella seconda il
quadrato dell'ipotenusa c . Il teorema di Pitagora è così dimostrato, con
tutta probabilità al modo di Pitagora .
|
|
|
La scoperta delle grandezze incommensurabili : crisi del pitagorismo
Il teorema di Pitagora che doveva rappresentare il vanto della scuola pitagorica si rivelò , invece , come il << cavallo di Troia del pensiero pitagorico>> . Infatti questo teorema contiene in sé la negazione dell’assioma che vuole le figure geometriche , come ogni oggetto esistente in natura , costituite da un numero finito di monadi . Il primo fatto geometrico che costrinse i pitagorici a riconoscere che le figure geometriche sono costituite da infiniti punti , è proprio connesso a quel medesimo teorema che porta il nome di Pitagora . Applicando detto teorema ad uno dei due triangoli isosceli in cui è diviso un quadrato , si dimostra facilmente che il lato e la diagonale di tale quadrato non possono avere alcun sottomultiplo comune , cioè la diagonale ed il lato di uno stesso quadrato sono grandezze incommensurabili .
Per avere rivelato la natura delle grandezze incommensurabili , Ippaso di Metaponto sarebbe stato scacciato ignominiosamente dalla scuola di Pitagora , ed a lui i pitagorici avrebbero eretto una tomba come ad un morto . Secondo la tradizione su di lui sarebbe caduta l’ira di Giove , il quale lo fece perire in un naufragio . La sua triste morte non impedì che lo scandalo si diffondesse rapidamente tra i cultori della matematica e finisse per scuotere dalle fondamenta l’intera concezione pitagorica .
La scoperta delle grandezze incommensurabili mette in crisi il pitagorismo , in quanto ne contraddice l’idea basilare , e pone fine all’illusione della possibilità di risolvere per via aritmetica i problemi geometrici . La geometria avrà in seguito uno sviluppo autonomo .
La prova dell’esistenza di grandezze incommensurabili apre una crisi di notevole portata , che si esprime nel profondo travaglio di pensiero legato al problema della divisibilità e della composizione delle grandezze geometriche .
Una crisi da cui si potrà uscire con la limitazione della validità dei concetti della matematica ad un solo ambito . Il dualismo tra continuità e discontinuità apparirà da questo momento nella sua entità di dilemma fondamentale e drammatico . Una difficoltà , legata alla comprensione dell’infinito , con la quale la mente umana dovrà misurarsi per secoli .
La crisi del pitagorismo verrà resa ancora più acuta dalla scoperta delle antinomie di Zenone sul movimento e sulla divisibilità . Per uscire da essa , i maggiori scienziati greci non troveranno altra via se non quella di scindere completamente la geometria dall’aritmetica , interpretando la prima come studio del continuo e la seconda come studio del discontinuo . Il rapporto tra continuo e discontinuo resterà , per tutta la storia del pensiero umano , un problema molto difficile e molto dibattuto; verrà , anzi , considerato come uno dei più astrusi << labirinti >> della ragione . . L’averne intuito l’esistenza e la difficoltà va considerato un merito , e molto notevole , dello spirito greco .