Equazioni differenziali del secondo ordine, lineari, a coefficienti costanti, omogenee.

La prima equazione di questo tipo, nota dalla meccanica, è l’equazione del moto armonico; infatti per questo moto la seconda legge della dinamica si scrive:

ma=-kx

in quanto la forza che genera questo moto è la forza elastica. Scritta in forma differenziale l’equazione si scrive

sempre dalla meccanica sappiamo che la soluzione di questa equazione è:

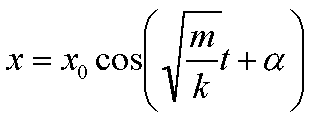
verifica:

Sostituendo nell’equazione data si vede facilmente che l’eguaglianza è verificata.

Dalla soluzione trovata risulta che l’ampiezza dell’oscillazione rimane invariata, e ciò equivale ad affermare che il moto dovrebbe continuare all’infinito con caratteristiche invariate. In realtà sappiamo che il moto si va smorzando più o meno rapidamente. Come correggere allora l’equazione? Nel moto di caduta dei gravi è stato aggiunto un termine contenente la velocità in quanto si è supposto che la forza frenante sia proporzionale alla velocità, è ragionevole supporre allora anche in questo caso che lo smorzamento dipenda dal mezzo (viscosità del mezzo), e sia proporzionale alla velocità (derivata prima dello spostamento) della massa oscillante.

Allora l’equazione assume la forma completa:

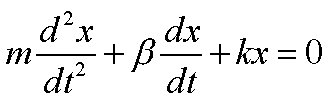
Come si risolve questa equazione? Che cosa succede se manca il termine in x (assenza di forza elastica)? e quando il secondo membro è diverso da zero?

Equazioni differenziali omogenee del II ordine a coefficienti costanti.

ay"+by'+cy=0

si cerca in primo luogo se esistono soluzioni del tipo y=e^kx

Poiché

y'=k e^kx

y"=k² e^kx

sostituendo:

(ak²+bk+c)e^kx=0

k deve dunque essere soluzione dell’equazione (equazione caratteristica):

ak²+bk+c=0

si possono allora presentare tre casi:

1) b²-4ac>0

in questo caso esistono due valori reali e distinti per k, k₁ e k₂, l’integrale generale è:

y=c₁e^k1x+c₂e^k2x

2) b²-4ac=0

in questo caso k₁=k₂=k e l’integrale generale si scrive:

y=(c₁+c₂x)e^kx

3) b²-4ac<0

in questo caso le radici sono immaginarie ; dette allora γ la parte reale e ω il coefficiente dell’unità immaginaria, l’integrale generale è:

y=e ^γx(c₁cos ωx+c₂sen ωx)

è proprio questo il caso più interessante, infatti la soluzione è una funzione periodica di ampiezza variabile con legge esponenziale; la quantità tra parentesi si può anche scrivere:

c₁(cos ωx+ sen ωx)

posto

= tgθ =

la precedente diviene:

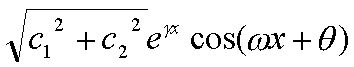
quindi l’integrale si può scrivere:

y= A(x)cos(ωx+θ)

funzione di ampiezza variabile e periodo .

Alla luce di queste considerazioni riprendiamo l’ esame dell’equazione, incompleta, del pendolo. Qui l’equazione caratteristica è:

α²+ =0

da qui la soluzione

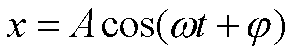
quindi la soluzione è un moto oscillatorio di ampiezza costante e periodo T=2π.

Il termine φ dipende dalla posizione iniziale.

Caso c=0

In questo caso, posto y'=z, y"=z' l’equazione si riconduce al primo ordine a variabili separabili:

a z'+bz=0

perciò, una volta trovato z l’equazione si risolve con una seconda integrazione.

Equazioni differenziali del II ordine a coefficienti costanti, complete.

Se il secondo membro è diverso da zero allora l’integrale generale è dato dall’integrale dell’omogenea associata al quale si aggiunge un integrale particolare dell’equazione data.

Trovare un integrale particolare non sempre è impresa facile, tuttavia vi sono alcuni casi in cui la ricerca è semplice.

1) il secondo membro è una costante, ad esempio:

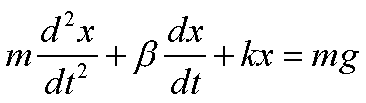
equazione del moto di caduta di un grave in un mezzo viscoso con forza elastica di richiamo.

Si pone x₁=.

Soluzioni possibili:

· le radici dell’omogenea associata sono reali e distinte, tenendo presente che sono entrambe negative in quanto i coefficienti dell’equazione caratteristica presentano due permanenze, l’integrale generale è:

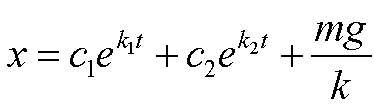
ma con k₁ e k₂ entrambi negativi il limite dei primi due termini tendono a zero per t che tende ad infinito, pertanto la massa m si avvicina alla posizione di equilibrio sia pure in un tempo molto lungo.

· le radici dell’omogenea associata sono coincidenti, allora l’integrale generale si scrive:

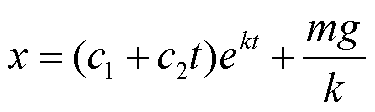
la soluzione non differisce dal caso precedente, al più la funzione presenta un massimo.

· le radici dell’omogenea associata sono immaginarie, in questo caso abbiamo:

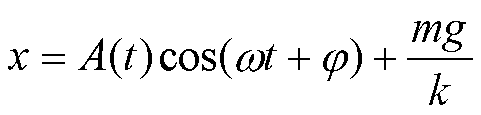
la massa m si ferma nella posizione di equilibrio ma compiendo attorno ad essa delle oscillazioni smorzate.

Un caso particolare è poi l’equazione:

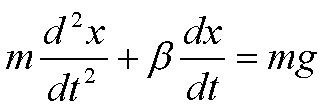
caduta di un grave in un mezzo viscoso.

Posto = v l’equazione diviene:

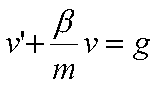
soluzione

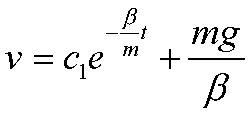
ponendo nell’istante iniziale v=0 si ottiene

c₁=-

quindi

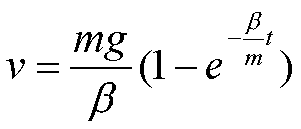
e infine:

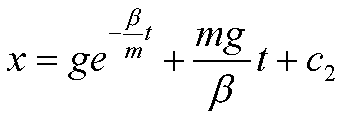
posto y=h per t=0 si ha c₂=h-g e quindi

2) il II membro è un polinomio in x, es.:

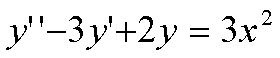
Si pone

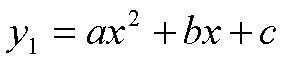
da cui

y'=2ax+b ; y"=2a e sostituendo

2a-6ax-3b+2ax²+2bx+2c=3x²

2ax²-(6a-2b)x+2a-3b+2c=3x²

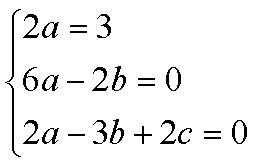
a=; b=; c=

integrale generale:

y=c₁e^x+c₂e^2x+x²+x+

3) il II membro è del tipo mcosωx+nsenωx , l’integrale particolare sarà

y₁=Acosωx+Bsenωx

con A e B costanti da determinare

4) Il II membro è del tipo ke^hx; un integrale particolare è ancora del tipo y₁=Ae^hx, con A e B costanti da determinare in modo da soddisfare l’equazione data se h non è radice dell’equazione caratteristica; se invece h coincide con una delle due radici allora y₁=Axe^hx; infine se h coincide con la radice doppia dell’equazione caratteristica allora si pone y₁=Ax²e^hx.

5) Il II membro è del tipo P_n(x)e^x, dove P_n(x) indica un polinomio di grado n in x. Si perviene ad un integrale particolare ponendo y₁=A_n(x)e^x, dove A_n(x) è ancora un polinomio di grado n in x, con le eccezioni come nel caso precedente.

Equazione differenziale del circuito RLC

Riprendiamo in esame l’equazione della scarica del condensatore:

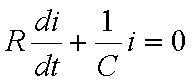
si può stabilire una interessante analogia tra questa equazione e quella del moto armonico smorzato; il termine contenente la derivata prima corrisponde alla resistenza del mezzo (in questo caso la resistenza elettrica del conduttore); il termine con la funzione incognita rappresenta la forza elastica di richiamo (qui assicurata dalla capacità), il termine con la derivata seconda, qui mancante, rappresenta l’inerzia della massa m. Ora ci domandiamo se è esiste in elettromagnetismo l’analogo dell’inerzia del moto. Ossia se un circuito elettrico ha la tendenza ad ostacolare variazioni della corrente da cui è attraversato e se questa proprietà dipende dalla derivata seconda. Sappiamo che un circuito elettrico attraversato da corrente genera un campo magnetico le cui linee di forza sono concatenate con il circuito stesso ed il cui modulo è proporzionale alla corrente medesima, per cui si può scrivere che il flusso del vettore B concatenato è a sua volta proporzionale alla corrente Ф(B)=Li.

Una variazione di corrente genera allora una forza elettromotrice indotta che, per la legge di Faraday-Neumann-Lenz è data da:

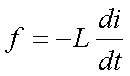
Circuito completo

Applico la legge di Ohm generalizzata:

V_A – – L- Ri = V_A

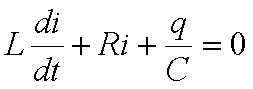
derivando termine a termine, anche se il secondo membro è una costante, si perviene a:

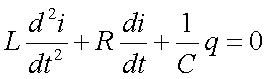
A questo punto l’analogia è evidente:

Quindi risolvere una delle due equazioni equivale a risolvere l’altra. È da notare ad ogni modo che l’integrale dell’omogenea associata in ogni caso è un termine tendente a zero quando la variabile tende ad infinito, in quanto le radici dell’equazione caratteristica sono negative entrambe, per cui rimane in definitiva solo l’integrale particolare. In particolare si può osservare che nel caso delle radici immaginarie, nel circuito elettrico si generano delle oscillazioni di frequenza

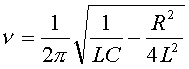
che nell’ulteriore condizione R=0, diventa

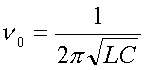
che è la frequenza propria di oscillazione del circuito.

Caso della forza elettromotrice sinusoidale.

L’equazione del circuito non cambia se è presente una forza elettromotrice costante. La soluzione indica la presenza di una corrente di carica del condensatore che tende a zero, al più può compiere delle oscillazioni (elettriche). Il caso più interessante si verifica quando la forza elettromotrice è di tipo sinusoidale f = f_o cosωt.

In questo caso un integrale particolare è del tipo

i(t)=i_osen(ωt+φ)

quindi una corrente sinusoidale di frequenza . Se dunque questa frequenza coincide con la frequenza propria di oscillazione del circuito si ha la risonanza e le oscillazioni diventano persistenti.

Esercizi:

y''-y = e^x

y''+3y'+2 y = 3

y'' +y'+2y = sen x

y''+2y'+2y = 2x+1

y''+2y'+y=e^-x

y''+4y'+3y=(x+2) e^-x