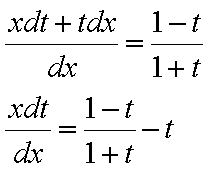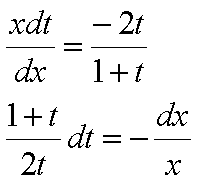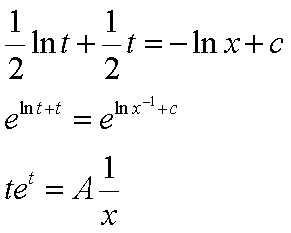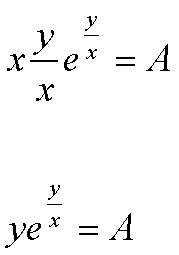Equazione della scarica

La caratteristica della curva di scarica è il periodo di dimezzamento; questa caratteristica si manifesta ogni qualvolta la variazione di una grandezza (la derivata) dipende dal valore istantaneo che quella grandezza assume.

Così nel caso della scarica:

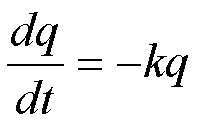
nel caso in questione l’ipotesi è giustificabile nel modo che segue. Consideriamo infatti un circuito di scarica RC; la d.d.p. disponibile è quella tra le armature del condensatore, che vale ; poiché il primo membro è l’intensità di corrente, allora ricordando la legge di OHM, la

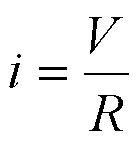
diventa:

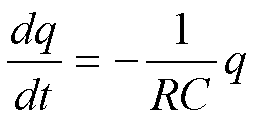
Equazione del primo ordine a variabili separabili

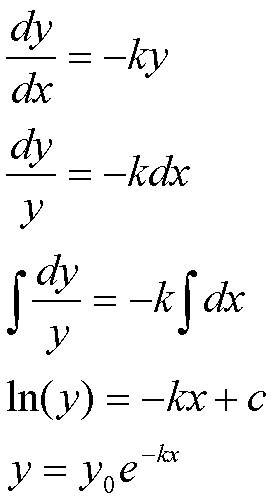
La soluzione

Dunque la soluzione è la seguente:

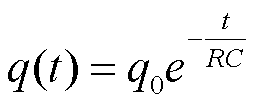
La corrente invece è la derivata della carica rispetto al tempo, quindi:

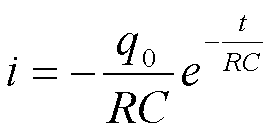
il segno negativo indica il verso della corrente; ma q₀=VC, e allora

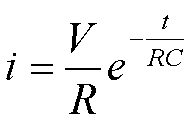
Periodo di dimezzamento.

La soluzione che abbiamo trovato deve essere in accordo con i fatti sperimentali osservabili, in particolare deve essere possibile mettere in evidenza l’esistenza di un periodo T di dimezzamento. Tale periodo T deve soddisfare quindi l’equazione:

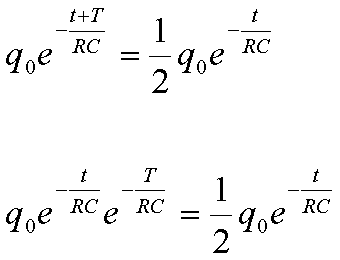
eliminando i fattori comuni:

Infine

T=RC ln2

Per verificare questo risultato si può analizzare la corrente di scarica mediante un oscilloscopio.

Altro caso interessante da analizzare è l’equazione della logistica: y'=ky(1-y/L)

Lineare del I ordine

y'+a(x)y=f(x) 1)

omogenea associata

y'+a(x)y=0

si risolve l’omogenea associata mediante separazione di variabili:

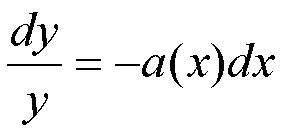
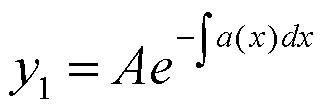
L’integrale generale della 1) è dato dall’integrale dell’omogenea associata a cui si aggiunge una qualsiasi funzione che la soddisfa (integrale particolare).

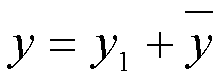
con

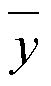
integrale particolare della 1).

Determinare un integrale particolare non sempre è semplice, tranne che in alcuni casi; ad esempio se il secondo membro è un polinomio in x, anche l’integrale particolare è un polinomio. Se il secondo membro è una funzione sinusoidale, si cerca un integrale particolare dello stesso tipo.

In alternativa si può applicare il metodo della variazione della costante arbitraria.

Supponendo y₁=A·f(x), si ha y₁'=A'f(x)+Af'(x) e sostituendo nella 1) si perviene ad una equazione in A', integrata la quale l’equazione è risolta.

Es.:

y'-xy = x

Si risolve l’omogenea associata y'-xy=0:

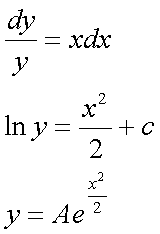
a questo punto si considera A come variabile, pertanto:

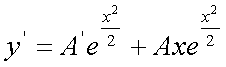
Sostituendo nella 1):

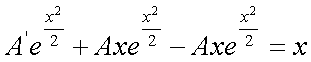
quindi

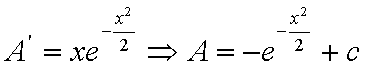
in definitiva:

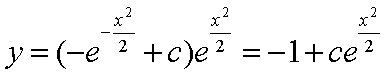
In questo caso però si può immediatamente osservare che un integrale particolare è –1, quindi

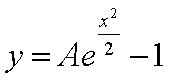
Altro esempio la legge di caduta dei gravi in presenza di un mezzo viscoso. Ammettendo che la resistenza del mezzo sia proporzionale alla velocità, l’equazione della dinamica si scrive:

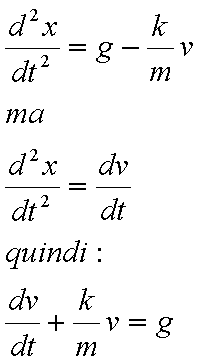
equazione lineare del primo ordine che ammette l’integrale particolare v = g.

Questo integrale particolare rappresenta il valore della velocità limite, costante, a cui tende v quando t tende ad infinito.

Come cambia la soluzione se si fa l’ipotesi che la esistenza del mezzo sia proporzionale al quadrato della velocità?

Equazione del tip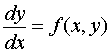o con f(x,y) omogenea di grado zero.

Si esegue il cambiamento di variabile y=tx, da cui dy=xdt+tdx e si sostituisce. Esempio:

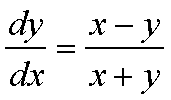
operando la suddetta sostituzione