Problemi del 5-3

1. Trovare la famiglia di curve per le quali la lunghezza del segmento di tangente tra il punto di contatto e l’asse y è uguale al tratto intercettato sull’asse y dalla stessa tangente.

La soluzione:

Posto OT=k si ha T(0, k), quindi

ma PT = TO = k, pertanto

elevando al quadrato I e II membro si ricava

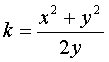
ma allora:

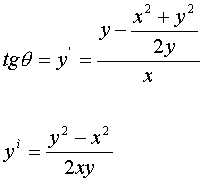
L’equazione così trovata è del tipo detto di Manfredi ed è integrabile mediante la posizione y=tx.

2. Determinare la curva avente la seguente proprietà:

a. La normale in ogni punto passa per l’origine degli assi.

la normale ha equazione:

Equazione integrabile mediante separazione di variabili.

b. Il segmento avente per estremi l’intersezione con l’asse x della retta tangente condotta per un punto P(x,y) ed il punto P stesso, forma un triangolo isoscele con il segmento PO.

dai dati del problema si ricava T(2x,0), quindi:

integrabile per separazione delle variabili.

c) La retta tangente in un suo punto P forma con la congiungente detto punto con l’origine degli assi un angolo costante.

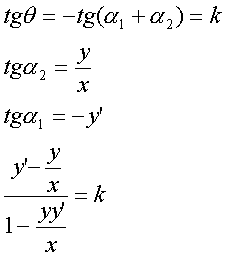
3. Per ogni punto P(x,y) di una curva passante per l’origine degli assi si traccino le parallele agli assi coordinati. Determinare la curva in modo che il rettangolo di diagonale OP resti diviso dalla curva in due parti, delle quali una è tripla dell’altra.

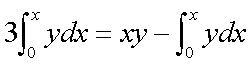
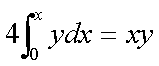
derivando I e II membro rispetto a x:

4y = y + xy'

3y = x y'

Integrabile per separazione delle variabili.

4. In una coltura di batteri il tasso di incremento è proporzionale al numero di batteri presenti. Se i batteri sono 10⁴ dopo 3 ore e 4x10⁴ dopo 5 ore, quanti erano all’inizio?

= k·N

5. Secondo la legge di Newton del raffreddamento, il tasso di raffreddamento di una sostanza a contatto con l’aria è proporzionale alla differenza tra la temperatura della sostanza e quella dell’aria. Se la temperatura dell’aria è 20° e la sostanza passa da 100°C a 80°C in cinque minuti, dopo quanto tempo la temperatura sarà di 25°C ?

= - k(T-T_a)

6. La velocità in una reazione chimica.

In una reazione chimica che avviene in una soluzione fino all’esaurimento dei reagenti, i due reagenti A e B si combinano formando una singola molecola del prodotto C a partire da una sola molecola di ciascun reagente. In base alla legge detta dell’azione di massa, la velocità con la quale procede la reazione è proporzionale al prodotto delle concentrazioni di A e di B nella soluzione (n molecole/cm³). Se a è la concentrazione iniziale di A e b quella di B, e detta x la concentrazione di C nell’istante t (x<a,b), la reazione procede con la velocità:

= k(a-x)(b-x)

7. Problema delle traiettorie ortogonali

Determinare le traiettorie ortogonali delle famiglie di curve:

a) x²+y² = a²; b) y² = ax; c) xy = a.

8. Determinare l’equazione della curva passante per Q(3 ;1) ed avente la seguente proprietà: il segmento della tangente alla curva in un suo punto P compreso tra questo punto e l’asse x è diviso a metà dal punto di intersezione con l’asse Y.

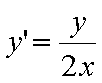
L’equazione è a variabili separabili.

Il passaggio per il punto Q si impone, dopo aver risolto l’equazione, per calcolare la costante di integrazione.