MATEMATICA
Sapendo che x + y = 30 e che x3 + y3 = 8100, quanto vale
x2 + y2 ?
A)
240 B) 120 C) 480
D) 210
E) 600
2)
Quanti 'zero' finali ha il prodotto dei primi 1000 numeri interi?
A)
200 B)
248 C) 250
D) 300
E) 1000
3)
Una fontana è alimentata da 6 getti che, da soli, la riempirebbero
rispettivamente in 1giorni, 2g, 2g, 3g, 3g e 3g.
A)
2 giorni B) 8 ore
C) 1 giorno D) 4 ore
E) 3 giorni
4)
Giovanni è un tipo forse troppo prudente, ha trascorso l'intero mese di
settembre in montagna ma è uscito dall'albergo solo 12 giorni, quando il
A)
9 B) 8 C) 6
D) 10 E) 12
5)
Una foglia magica, avente la superficie di 1 cm2 , cade in uno stagno ed ogni
giorno raddoppia la sua superficie. In 100 giorni lo stagno è perfettamente
ricoperto. Se inizialmente fosse caduta una foglia di 2 cm2 in quanti giorni
lo stagno si ricoprirebbe?
A)
1 giorno in più B) 1
giorno in meno C) 3
giorni D) 2 giorni in meno
E) 1 giorno
6)
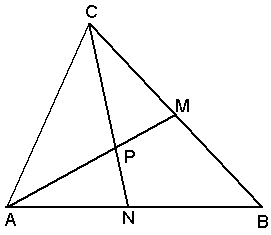
Nel triangolo in figura AM e CN sono due mediane.Quanto vale l'area del
triangolo rispetto al triangolo ABC?
A)
½ B) ¼ C) 1/6 D)
1/8 E)
1/12
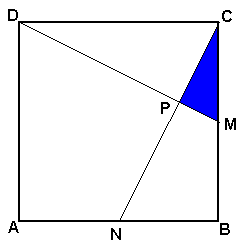
7) Quale è il rapporto tra l'area del triangolo CPM
e quella del quadrato ABCD dove M e N sono i punti medi dei lati BC e AB?
A) 1/20
B) 1/10
C) 1/ 5
D) 1/8 E) 1/ 12
8)
In un supermercato arrivano tre casse sigillate con le seguenti etichette
"LIMONI" " MELE" e "LIMONI E MELE" .
A)
1 B) 2
C) 4 D) 3
E) 6
9)
Se i numeri 0,3 ; 0,3
; (0,3)2
; 1/ (0,3) ; 1/
0,3; 1/0,3
vengono messi in ordine crescente, il terzo numero è:
A)
0,3 B) 0,3
C) (0,3
)2 D) 1/0,3
E) 1/0,3
10
) Vi sono tre circonferenze tangenti esternamente a due a due. Esse hanno
raggio uguale rispettivamente a 1,2 ,3. Il raggio della circonferenza
circoscritta al triangolo che ha per vertici i tre centri delle circonferenze
è allora uguale a :
A)
2 B)
2,5 C) 3
D)
E) non è possibile
determinarlo
11)
Un poligono regolare ha n lati e 4n diagonali. Quanto vale n?
A)
8
B) 9 C) 109 D) 11
E) 12
12)
Sappiamo che una sola delle tre seguenti relazioni è vera x=5 ,
x>5 , x
5. Quali delle seguenti affermazioni è sicuramente vera?
5 C) x>5
D) x<5 E) x
13)
Dati cinque interi consecutivi, cosa si può dire della cifra delle unità del
loro prodotto?
A)
Può essere qualunque
cifra
B)
Può essere qualunque
cifra pari
C)
Può essere 0 oppure
5
D)
E' sempre 0
E)
Nessuna delle
precedenti
14)
Quanto vale il quadrato del quadrato del quadrato di 8?
A)
28;
B) 83 C) 86;
D) 88 E)
254
15)
Ad un torneo di golf partecipano 256 concorrenti. Il torneo prevede che ad
ogni turno partecipino 4 concorrenti:il vincitore passa il turno successivo
mentre gli altri tre vengono eliminati.Quanti turni sono necessari per
individuare il vincitore assoluto del torneo?
A)
16 B) 64 C) 65 D)
85 E) 128
16)
Quanti angoli maggiori di 90° può avere un quadrilatero non
intrecciato?
A)
ne ha sempre almeno
uno
B)
ne ha al più uno
C)
ne ha al più due
D)
ne ha al più tre
E)
può averne quattro
17)
Quale tra le seguenti
espressioni rappresenta la metà di 41998?
A)
21998 B) 41997; C) 2999; D) 4999;
E) 23995
18) Sia G il baricentro del triangolo ABC. Sapendo che AB < AC < BC, quale tra i triangoli GAB, GAC, GBC ha area massima ?
A) GAB; 2) GAC ; C) GBC ; D) hanno tutti la stessa area E) dipende dalla lunghezza dei lati di ABC
19) In un rombo di area 80 cm2 una diagonale è il doppio dell'altra. Quanto è lungo il lato del rombo
A)
8
cm. B)
cm.; C) 10 cm.
C) 20 cm. D) non si
può determinare
20) Lunedì ho acquistato delle azioni che martedì hanno perso il 10% del loro valore e mercoledì hanno guadagnato il 10% rispetto a martedì. Immediatamente ho venduto le mie azioni. Rispetto al prezzo iniziale il prezzo finale è:
A) lo stesso B) diminuito dell' 1% C) aumentato dell' 1% D) diminuito del 10%; E) aumentato del 10%