INTEGRALI INDEFINITI
I. - Integrale indefinito di una funzione continua.
Assegnate due funzioni f(x) e g(x) diremo che g(x) è una funzione primitiva di f(x)
se g(x) à una funzione la quale, in ogni punto dell'intervallo [a, b], ha per derivata f(x):
g(x) primitiva di f(x)![]() g’(x)=f(x)
g’(x)=f(x)
Ad esempio, la funzione senx è una primitiva di cosx, perchè risulta: Dsenx = cosx.
- Se g(x) è una primitiva di f(x), anche g(x) + c, dove c è una costante arbitraria, è una primitiva di f(x), perchè si ha :
D[g(x) + c] = Dg(x) + D c = g'(x) + 0 = f(x) .
Inversamente, se h(x) è una primitiva di f(x), diversa da g(x), risultando
h’(x)= f(x) , g’ (x) = f(x) , si ha
h’(x) = g’(x);
quindi le due funzioni h(x) e g(x), per un noto teorema di analisi matematica, ( 2° corollario del teorema di Lagrange)differiscono per una costante, e perciò
h(x) = g(x) + k.
Da ciò segue che se f(x) possiede una primitiva ne possiede infinite e questo sono espresso tutte dalla formula:
g(x) + c,
dove e è una costante che può assumere qualunque valore reale.
Chiamasi integrale indefinito della funzione f(x), e si indica con la notazione
![]() f(x)dx
f(x)dx
la totalità delle funzioni primitive della f(x)
L'integrale indefinito di una funzione dipende quindi da una costante additiva c.
![]() f(x)dx=
g(x)+c
f(x)dx=
g(x)+c
Dalle cose dette segue
D![]() f
(x)dx = D[g(x)+c]= g’(x)=f(x)
f
(x)dx = D[g(x)+c]= g’(x)=f(x)
L'operazione di integrazione indefinita appare così come l'operazione inversa della derivazione.
Si dimostra che
Ogni funzione continua in un intervallo ammette sempre primitive.
Sicchè, mentre l'operazione di derivazione non può applicarsi a tutte le funzioni continue, l'operazione inversa può invece applicarsi a tutte le funzioni continue.
Sono immediate le seguenti proprietà degli integrali indefiniti:
a)
Se k è una costante qualunque, si ha
∫
k f(x) dx = k∫f(x) dx
cioè : l'integrale del prodotto di una costante per una funzione continua è eguale al prodotto della costante per l'integrale della funzione.
2a) Se f1(x), f2(x) ......fn(x) sono n funzioni continue, si ha
∫
[f1(x) + f2(x) + fn(x)] dx = ∫f1(x)dx +∫f2(x) dx+……∫fn(x) dxcioè, : l'integrale di una somma di funzioni continue è eg uale alla somma degli integrali delle singole funzioni.
Integrali indefiniti immediati.
Se mediante le nozioni già acquisite nel calcolo differenziale si riconosce che f(x) è la derivata della funzione g(x), l'integrale indefinito di f(x) è immediato, essendo :
∫
f(x)dx = g(x) + c ,
con e costante arbitraria. E’ appunto così che si ottengono i seguenti integrali, che vanno ricordati a memoria:

Proviamo con qualche esempio:
![]() +
c
+
c
![]()

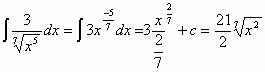 +c
+c
![]()

![]()
![]()
Integrali quasi immediati o generalizzati
Si consideri il seguente integrale:
∫
(2x-5)6dxE’ certamente un integrale che a che fare con quello della potenza. Potremmo, in linea di principio, svilupparlo secondo regole algebriche note, ma il "disagio" è evidente.
Sappiamo che:
∫
xn dx=Al posto di x, nel nostro caso, figura: φ(x) = (2x-5). La regola generale è allora la seguente:
Se al posto di x figura φ(x), se cio
è la funzione da integrare è una funzione composta, occorre che sotto il segno di integrale figuri anche la sua derivata φ’(x).La (1) diviene allora:
∫ [φ(x)]n
φ’(x) dx=∫ [φ(x)]nd
( φ(x))=
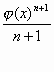 +c
(2) E’ facile infatti verificare che
+c
(2) E’ facile infatti verificare che
D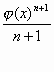 =
[φ(x)]n
φ’(x).
=
[φ(x)]n
φ’(x).
Nel nostro caso manca la derivata di 2x+5. Ma:
D ( 2x+5)=2.
Posso allora scrivere:
∫
(2x-5)6 dx=Dunque, se si tratta di un numero, e solo se si tratta di un numero, è possibile moltiplicare e dividere per quel numero.
Consideriamo quest’altro esempio:
∫
Si può scrivere:
∫
Si tratta ancora di un integrale del tipo (2). Questa volta la derivata figura direttamente. Possiamo allora scrivere:
∫
 +c
+c
Ecco il quesito proposto l’anno scorso agli esami di stato:
![]()
Si tratta dell’integrale della f potenza, per n=1
Si ottiene pertanto, immediatamente:![]() =
=![]()
Ci chiediamo ora se è possibile generalizzare le osservazioni fatte a tutti gli integrali immediati.
La risposta è sì:
Se al posto di x figura φ(x), ovvero una funzione del tipo f(φ(x)), occorre che sotto il segno di integrale figuri φ’(x).
Un caso importante è il seguente:
∫
![]()
Ecco un caso interessante: se al numeratore compare la derivata del denominatore, l’integrale è quello del logaritmo del denominatore.
Ad esempio:
![]()
∫
tg(x) dx= ∫[sin(x)/cos(x)] dx = -logIl procedimento si può dunque generalizzare a tutti gli integrali immediati. Ecco la nuova tabella:

Ecco qualche esempio relativo:
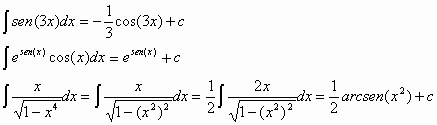
Esiste qualche metodo per individuare di che integrale si tratta?
Serve, com’ è evidente, innanzitutto una buona dose di intuito. Ma si può anche articolare un ragionamento più logico.
Consideriamo ad esempio il seguente integrale:
![]()
Dobbiamo porci alcune domande:
CERCA L’INDIZIO!
Ad esempio: se figura una potenza o una radice potrebbe trattarsi dell’ integrale della potenza; un rapporto, integrale del logaritmo; al denominatore 1+ f2, integrale dell’arcotangente…Sembra essere il nostro caso!
Posso allora concludere che:
![]() =
-arctg (cos(x)) +c
=
-arctg (cos(x)) +c
METODI DI INTEGRAZIONE
Esamineremo diversi metodi che servono a ricondurre gli integrali dati ad altri già noti o più facilmente calcolabili. Occorrerà spesso applicare opportuni artifici.
INTEGRAZIONE PER DECOMPOSIZIONE
Consiste nel decomporre la funzione che si vuole integrare nella somma algebrica di funzioni delle quali sia noto l’integrale. Facciamo qualche esempio:
![]() =
=
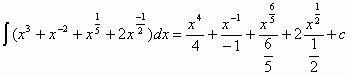 =
=
![]()
![]() =
=
![]() =
=
=![]()
![]()
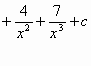
![]() =
=
![]()
![]()
Conviene procedere utilizzando le formule di bisezione:
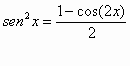
Allora:
![]() =
=
![]()
![]()
![]()
Nel seguito svolgeremo questo integrale anche con altri metodi. Per ora conviene osservare che:
![]() =
=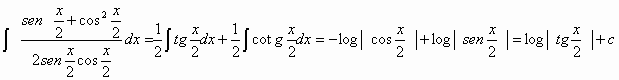
INTEGRAZIONE PER PARTI
E’ un metodo che ci consente di intervenire sulla integrazione del prodotto di due funzioni. Vale infatti la seguente formula generale:
![]() (1)
(1)
Dimostriamo inanzitutto la relazione, che scaturisce dal teorema della derivata del prodotto.
Infatti:
D f(x) * g(x) = f ‘ (x) * g(x) + f(x) *g’(x) . Da essa risulta:
f (x) * g’(x) = D[ f(x) * g(x)] – f’(x) *g(x).
Passiamo all’integrale:
∫
f (x) * g’(x) dx = ∫D[ f(x) * g(x)] dx -∫ f’(x) *g(x) dx, da cui, osservando che :∫
D[ f(x) * g(x)] = f(x) * g(x), la (1)
Osserviamo attentamente il primo membro della (1). Figurano due funzioni.
La prima, f(x) è detta fattore finito. Di essa occorre conoscere f ‘(x), ovvero la derivata
La seconda, g ‘ (x) , è detta fattore differenziale. Di essa occorre conoscere g(x), ovvero la primitiva.
L’integrale risulterà di facile svolgimento se la scelta delle due funzioni è appropriata.
Possiamo ad esempio dire che, se figura una potenza, essa va scelta in generale come fattore finito
( a meno che non figuri insieme al logaritmo..e non solo…).
Procediamo con opportuni esempi:
∫
x2 * ex dxScegliamo f(x) = x2
![]() f
‘ (x) = 2x
f
‘ (x) = 2x
g’(x)= ex![]() g(x) = ex . Risulta allora:
g(x) = ex . Risulta allora:
∫
x2 * ex dx = x2 * ex - ∫2x* ex dx = x2 * ex – 2∫x* ex dx . (2)Possiamo ancora procedere per parti.
f(x) = x
![]() f
‘ (x) = 1
f
‘ (x) = 1
g’(x)= ex![]() g(x) = ex .
g(x) = ex .
Pertanto: ∫x* ex dx = x* ex - ∫ex dx = x* ex - ex + c
E, sostituendo nella (2) si ottiene infine:
∫
x2 * ex dx = x2 * ex - 2∫x* ex dx = x2 * ex – 2 x* ex + 2 ex +c
∫
x* cos (x) dxScegliamo : f(x) = x![]() f
‘(x) = 1
f
‘(x) = 1
g ‘(x) =cos x![]() g(x)
= sen x
g(x)
= sen x
Pertanto: ∫x* cos (x) dx = x* sen x - ∫sen x dx = x* sen x + cos x +c
∫
x2 *2x dx
f(x) = x2
![]() f
‘ (x) = 2x
f
‘ (x) = 2x
g ‘(x) = 2x
![]() g(x)
=
g(x)
=![]() .
Pertanto:
.
Pertanto:
∫
x2 *2x dx = x2 *Integriamo ancora per parti :
f(x) = x
![]() f
‘ (x) = 1
f
‘ (x) = 1
g ‘(x) = 2x
![]() g(x)
=
g(x)
=![]()
Allora:
∫
x* 2x dx = xrisultato che basta sostituire nella ( 3).
Osserviamo ora il seguente integrale:
![]()
In questo caso conviene scegliere:
f( x) = log x ( non ne conosciamo infatti la primitiva, ma la
derivata!)
![]()
g’(x) = x2![]() g
(x) =
g
(x) =
![]()
Allora:
![]() = log x *
= log x *
![]() -
-
![]() log x *
log x *
![]() -
-
![]() log x *
log x *
![]() -
-![]()
E, finalmente, siamo in grado di calcolare :
![]()
Dove sono le due funzioni ? Semplice:
![]() =
=
![]()
Sceglieremo perciò:
f(x) = log x![]() f’(x)
=
f’(x)
=
![]()
![]()
g’(x) = 1![]() g(x)
= x
g(x)
= x
Allora:
![]() =
x * log x -
=
x * log x -
![]() x * log x- x + c
x * log x- x + c
In modo analogo:
![]()
![]() dx=
x * arctgx-
dx=
x * arctgx-
![]()
avendo scelto: f(x) = arctg x f’ (x) =
![]()
g’(x) =1 g(x) = x
![]()
E, poiché D ( 1-x2) = -2x , moltiplico e divido per -2
= x*arcsen x +![]()

Terminiamo con un caso interessante di integrazione per parti, fondato su un procedimento di iterazione
![]()
![]() Si
può scegliere indifferentemente l’una o l’altra funzione come fattore finito.
Scegliamo:
Si
può scegliere indifferentemente l’una o l’altra funzione come fattore finito.
Scegliamo:
f(x) = ex f’ (x) = ex
g’(x) = sen x g(x) = -cos x
Pertanto:
![]() = - ex* cos x + ∫ex
cos x dx
= - ex* cos x + ∫ex
cos x dx
Continuando:
f(x) = ex f’ (x) = ex
g’(x)= cos x g(x)= sen x
Allora:
![]() = - ex* cos x + ∫ex
cos x dx = - ex* cos x+ ex sen x -
∫ex sen x dx
= - ex* cos x + ∫ex
cos x dx = - ex* cos x+ ex sen x -
∫ex sen x dx
A secondo membro compare lo stesso integrale del primo membro, cambiato di segno. Trasportiamolo a primo membro!
2![]() =-
ex* cos x+ ex sen x
=-
ex* cos x+ ex sen x
e, dividendo per 2:
![]() =
=![]()
Nello stesso modo si può svolgere un integrale del tipo:
![]() o del tipo :
o del tipo :
![]() ,
osservano che :
,
osservano che :
![]() ovvero :
ovvero :
![]() ,
e scegliendo un fattore come fattore finito, l’altro come fattore differenziale.
,
e scegliendo un fattore come fattore finito, l’altro come fattore differenziale.

Integrazione delle funzioni razionali fratte.
![]()
![]()
Quando il grado della funzione al numeratore è maggìore o eguale a quello della funzione al denominatore, la funzione razionale dicesi impropria ; nel caso opposto dicesi propria.
Se la funzione razionale è impropria si può allora effettuare, la divisione secondo le regole dell'algebra e se Q(x) indica il quoziente e R(x) il resto della divisione, abbiamo :
M(x) = N(x)Q(x) + R(x);
E divìdendo ambo i membri per N(x):

e perciò:

Sappiamo già calcolare ∫Q(x)dx e ci resta quindi da calcolare
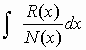
dove R(x) è una funzione razionale intera dì grado inferiore a quello di N(x). Si vede così che l'integrazione di una funzione razionale impropria viene ricondotta all'integrazione di una funzione razionale intera e dì una funzione razionale propria. Basta quindi che ci occupiamo dell'integrazìone delle funzioni razionali proprie.
A tale scopo si dimostra, come è noto, la possibilità di integrare queste funzioni con un metodo generale che consiste nel decomporre la frazione data in una somma di frazioni che sappiamo integrare con i procedimenti già noti. In particolare faremo in modo di far sempre riferimento a funzioni razionali fratte del tipo:
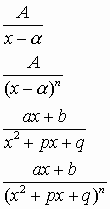
che chiameremo FRATTI SEMPLICI
Chiariremo il metodo con alcuni esempi e a tale scopo dìstingueremo i seguenti casi:
a) Caso delle radici reali e distinte.
Consideriamo la funzione razionale propria:
![]()
e supponiamo che l'equazione di grado n:
N(x)=0
abbia tutte le n radici reali e distinte:
![]()
In questo caso si dimostra che è sempre possibile determinare, e
in modo unico, n costanti A, B, C….N in modo che valga l'identità:

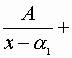

In base a questa decomposizione l'integrale della funzione
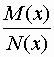
risulta eguale alla somma di n integrali che sappiamo calcolare perchè, come è, noto, corrispondono al logaritmo.
Chiariamo il procedimento con qualche esempio.
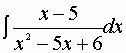
Vale la scomposizione: x2-5x+6=(x-2)(x-3).
Si tratta allora di determinare due costanti A e B in modo che sia valida l’identità:
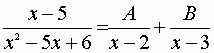 (1)
(1)
Possiamo procedere in due modi:
A)Eliminiamo i denominatori:
x-5 = A(x-3)+B(x-2) (2)
Assegniamo alla x, rispettivamente, i valori che annullano le singole parentesi:
Per x=3 -2= B
Per x=2 -3=-A![]() A=3
A=3
B) Sviluppando nella (2) i calcoli a secondo membro e ordinando:
x-5 = Ax -3A + Bx- 2B=x(A+B) -3A-2B
e, ricordando il PRINCIPIO DI IDENTITA’ DEI POLINOMI, il quale afferma che due polinomi sono uguali se e solo se lo sono i coefficienti delle potenze dello stesso grado:

![]() A=3
B =-2
A=3
B =-2
Non ci rimane che sostituire nella (1) e passare all’integrale di ambo i membri:
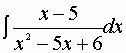 =
=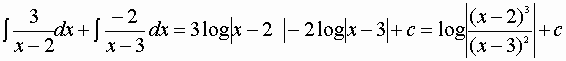

Studiamo l’identità:
 =
=
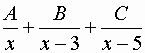 (**)
(**)
x2 -1 = A( x-3) (x-5)+ Bx (x-5)+ Cx (x-3)
Sviluppando con il secondo metodo:
x2-1 = x2 (A+B+C)+x(-8A-5B-3C) +15A
Da cui:
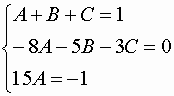
![]() A= -
A= -
![]() B=
B=![]() C=-
C=-![]()
Sostituendo nella (**) e passando all’integrale, si ottiene:
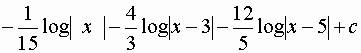
Esaminiamo ora il caso in cui
IL denominatore ammetta radici reali e multiple
Supponiamo cioè che l’equazione
N(x)=0
non abbia tutte le radici distinte, pur essendo sempre reali. Supponiamo, cioè, tanto per fissare le idee, che risulti:
N(x) = (x-α
1)n (x-α2)m.Nella decomposizione in somma, allora, procederemo così:

utilizzando cioè al numeratore tante lettere per quant’è l’ordine della radice multipla.
Un esempio renderà tutto più chiaro:
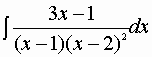
Studiamo l’identità:
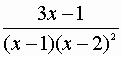 =
=
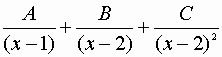 (°°)
(°°)
da cui, procedendo nel modo usuale:
3x-1= A (x-2)2+ B(x-1)(x-2) +C(x-1)
3x-1 = x2 (A+B)+ x( -4A-3B+C)+ (4A+2B-C)
e, risolvendo il sistema che si ottiene, si ricava:
A=2 B=-2 C=-5
E, sostituendo nella (°°) e passando all’integrale:
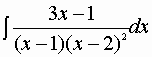 =
=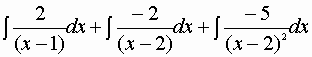 e qui occorre osservare la novità della presenza, oltre dei due consueti
logaritmi, di un integrale della funzione potenza:
e qui occorre osservare la novità della presenza, oltre dei due consueti
logaritmi, di un integrale della funzione potenza:
= 2 log![]() -5
-5![]() log
log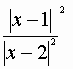 -5
(x-1)-1 +c
-5
(x-1)-1 +c
CASO DELLE RADICI COMPLESSE
Prima di affrontarlo in generale, esaminiamo un caso del tipo:
![]() con
con
![]() .
(§)
.
(§)
Si tratterà in tal caso, con opportuni e semplici artifici, di
ricondurlo a un integrale del tipo:
 .
.
Procediamo con un esempio:
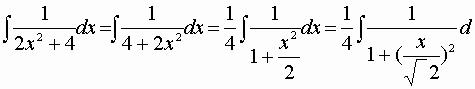
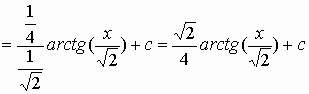
procedimento standard…scriviamo al denominatore prima il numero, poi il quadrato..numero in evidenza…riscostruiamo il quadrato..moltiplichiamo e dividiamo per la derivata della base…
Ma come procediamo se il trinomio al denominatore è completo, e
![]() ?
?
Basta osservare che : x2+px+q=x2+px+ p2/4- p2/4+q= (x+p/2)2+(-p2/4+q), che è ancora la somma di un quadrato con un numero, come nel caso (§).
Ecco un esempio che, speriamo, renderà tutto più chiaro:
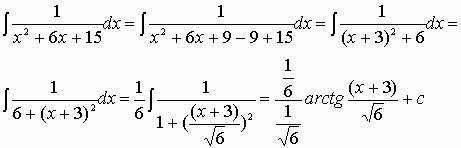 (§§§)
(§§§)
Possiamo ora, prima di generalizzare, considerare questo caso molto interessante:
 con il
con il
![]() .
(5)
.
(5)
La regola generale è quella di, con opportuni artifici, COSTRUIRE, AL NUMERATORE LA DERIVATA DEL DENOMINATORE E DI DECOMPORRE IN SOMMA.
Si otterrà in ogni caso la somma di un logaritmo e di un
arcotangente, se
![]() ,
ovvero di un logaritmo e di una potenza, se
,
ovvero di un logaritmo e di una potenza, se
![]() .
.
Ecco un esempio:
 e
l’ultimo integrale è del tipo (§§§) facilmente riconducibile a un integrale
dell’arcotangente.
e
l’ultimo integrale è del tipo (§§§) facilmente riconducibile a un integrale
dell’arcotangente.
E’ possibile fornire anche una formula valida in generale:
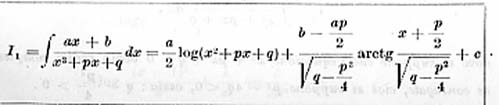
Passiamo infine al caso generale. Cosa accade se uno dei
fattori, di secondo grado, non è scomponibile, dunque non ammette radici reali (![]() )?
)?
In tal caso, al numeratore, al posto di una lettera del tipo A, B, C,..si utilizzerà un binomio di 1° grado .
 (5).
(5).
Per concludere…scherzosamente, ecco un bell’integrale rompicampo:
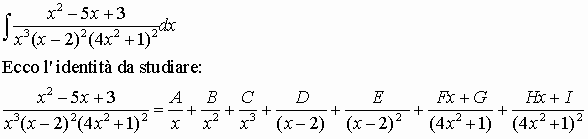
..ricchi primi a chi riesce a calcolare correttamente i valori delle 9 costanti!!
Integrali per sostituzione
Si tratta di una vasta gamma di integrali, per i quali è indispensabile prima una opportuna sostituzione.
Avviene talvolta che il calcolo di un íntegrale:
∫
f(x)dx ,
si semplifica quando si cambia la variabile d'integrazione x con un'altra variabile t legata alla precedente da una opportuna relazione.
In pratica, fissata la sostituzione x=α(t), essendo tale funzione derivabile e dotata di inversa:
t=
![]() (x),
si calcola il differenziale della x: dx = α’(t)
dt e quindi nell’integrale assegnato alla x e alla dx si sostituiscono le
loro espressioni.
(x),
si calcola il differenziale della x: dx = α’(t)
dt e quindi nell’integrale assegnato alla x e alla dx si sostituiscono le
loro espressioni.
Il nuovo integrale, tutto riferito alla variabile t, è in genere di più facile risoluzione.
Calcolato tale integrale, si sostituisce al posto di t il suo valore e il risultato è finalmente espresso nella variabile iniziale x.
Naturalmente non esiste la possibilità di riconoscere in ogni caso quale sia la sostituzione migliore.
Possiamo comunque offrire una ampia gamma di casi che possono essere utili.
INTEGRALI DEL TIPO f![]()
Consideriamo ad esempio il seguente integrale:
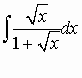 (1)
(1)
Conviene porre:
![]() =t
=t
Il procedimento, dopo la posizione fatta, è poi il seguente:
1) Si ricava la x x= t2
2) Si passa al differenziale di ambo i membri: dx= 2t dt.
Sostituendo nella (1) si ottiene:

Integrali del tipo:
![]()
Si pone:
![]()
ES:
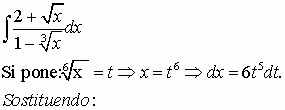

Ecco un integrale molto interessante:
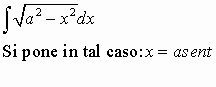
![]()
Integrali del tipo f( x, ex)
Si pone, in tal caso: ex=t.
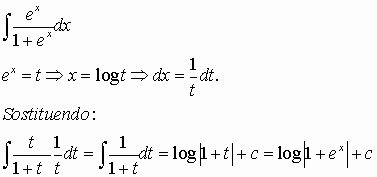
Naturalmente, la regola non è generale.
Ad esempio, nell’integrale: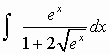
converrà porre
![]()
mentre nell’integrale:
![]()
converrà porre:
![]()
Si tratta, come è evidente, di affidarsi spesso a un buon intuito, nonché alla consapevolezza di ottenere, dopo la sostituzione, un integrale il più semplice possibile.
Va aggiunto che tutti gli integrali, che noi preferiamo risolvere come integrali quasi immediati, possono essere risolti per sostituzione.
Ad esempio:

Passiamo ora ad esaminare due vastissime gamme di integrali risolvibili con opportune sostituzioni. Ci limiteremo ad alcuni esempi , solo per dare un "assaggio" della grande varietà di casi.
Integrazione di alcune funzioni trascendenti
A tale gruppo appartengono gli integrali in cui figurano, con potenze opportune, le note funzioni goniometriche sen x, cos x, tg x che, per convenienti sostituzioni, possono trasformarsi in integrali di funzioni razionali.
Ecco alcuni casi possibili:
![]()
In tal caso ricordando che
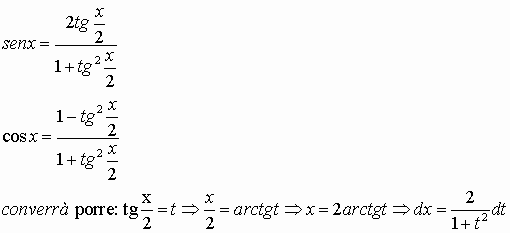 ,:
,:
con queste sostituzioni, un integrale del tipo:
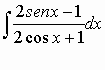
si trasforma in un usuale(!!) integrale di funzione razionale fratta.
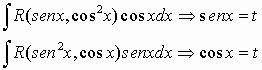
![]()
![]()
Nel primo caso, cioè, converrà esprimere tutto in coseno, nel secondo tutto in seno, mentre nel terzo caso di espressione omogenea di 2° grado in seno e coseno, tutto in tangente, ricordando che:
 (***)
(***)
Ad esempio:
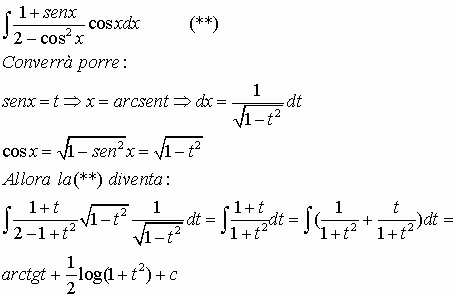
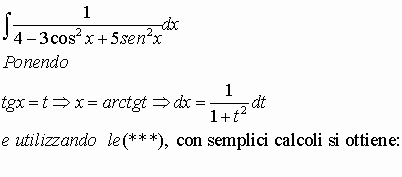
![]()
Integrazione di alcune funzioni irrazionali
Anche questo è un campo vastissimo. Noi ci limitiamo, oltre ai casi già trattati, ad altri due casi indubbiamente utili che, va subito premesso, portano però a calcoli in genere molto lunghi.

Ecco un esempio:
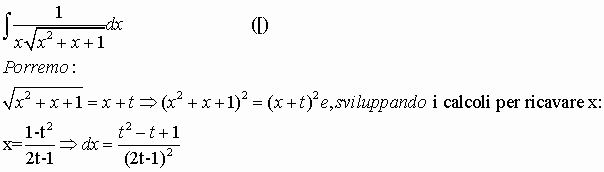
Non ci resta(..si fa per dire…) che sostituire nella
![]() e
fare i calcoli.
e
fare i calcoli.
Otterremo alla fine:![]()
di risoluzione davvero facile.
E’ utile osservare, a consolazione dei naviganti nel mare degli integrali, che se nella tabella degli integrali immediati avessimo aggiunto, come spesso si suole fare, i seguenti integrali:
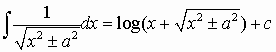
allora gli integrali del tipo:
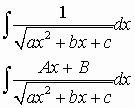
si possono risolvere riducendo il denominatore, con opportuni artifizi, alla somma o alla differenza di un quadrato con un numero. Ma su ciò aspettiamo lumi dagli alunni più bravi.